Beauty of Math
BY MEI SHAO '25
|
The day that you receive a 73 on your math test arrives—again. You vow that once you graduate, you’ll never touch math again.
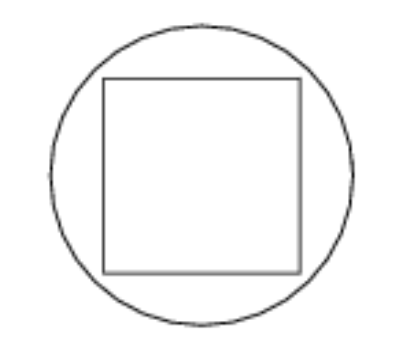
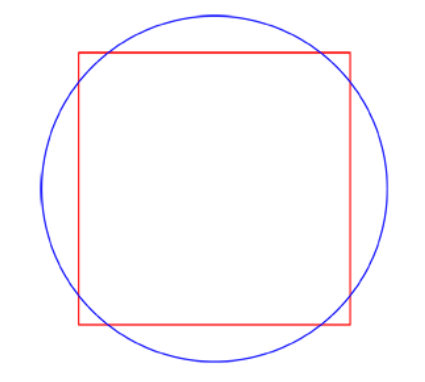
But wait! School math isn’t the only math out there! Many students are blinded by the drudgery of the school math curriculum that they overlook the complex and mesmerizing math world, along with the invaluable life skills it teaches you. Today, I will present you with two of my favorite math problems in a bid to change your mind. A square of side length 1 and a circle of radius (√3)/3 share the same center. What is the area inside the circle, but outside the square? First, let’s visualize this problem. It looks simple enough. Just subtract the areas. But that’s wrong! Many of us have already learned that math is cheeky. For me, this question epitomizes the ease of making an error. Though mathematics consists of a set of rigid rules, there still exists an extraordinary amount it can hide. Look beneath the surface! Let’s investigate the diagonal of our square. Using the Pythagorean theorem, we discover that the distance between the center of the square and the vertex of the square is √2/2. But, that’s longer than the circle’s radius! So our diagram actually looks like this. The point is, math is sneaky. Though you may hate it for that reason, there’s always a method to the madness. Math teaches you to persevere for that sweet feeling of having solved another enigma.
Compute the sum 1 - ½ + ⅓ - ¼ + ⅕ -⅙ …. (alternating harmonic sequence) Instead of tackling the beast first, consider a simpler version of our problem: an alternating series of ones: 1-1+1-1+1…. By grouping terms together, we can cancel things out: (1-1)+(1-1)+(1-1)... OR 1-(1-1)-(1-1)... If we group it differently, we get two different results: 0 or 1. Which one is it? If this sequence ended, this wouldn’t be an issue. However, since this is an infinite sequence, mathematicians have decided that the answer is neither 0 nor 1. Our sum of alternating 1’s was declared “divergent,” never converging on one answer. With the first steps taken, let’s return to our original task. Does it converge? If we add everything, we find that it does converge at a number near 0.69. Have we done it? Remember, math is sneaky. Let’s try to rearrange our sum. 1 - (12) - (¼) + (⅓) - (⅙) - (⅛) + (⅕) - (⅒) - (1/12)... (1 - ½) - ¼ + (⅓ -⅙) - ⅛ + (⅕ - (⅒)) - (1/12)... ½ - ¼ + ⅙ - ⅛ + ⅒ - 1/12… ½ (1 - ½ + ⅓ - ¼ + ⅕…) It’s the alternating harmonic series! Again? Somehow, we’ve halved the sum. Why is it different? Although this series converges, it diverges if we regroup the terms. Thus, the alternating harmonic series is branded as “conditionally convergent.” Mathematicians continue to explore such sums, and they pop up everywhere. Infinity, which seemed like a daunting prospect, revealed itself as we discovered rules and theorems to tame it. Math teaches us that a journey of a thousand stages starts with a single step. Now that we’ve arrived at the frontier of math, where to next? That’s for you to decide! So many secrets have been unearthed, and many more remain hidden. If these problems made you curious for more, I implore you to go beyond these samples. Online wikis like “The Art of Problem Solving” provide a great source for both theories and problems to get the cogs turning. Dive into the beautiful world of mathematics! |